LeetCode - Container With Most Water

Problem description

description

Given n non-negative integers a₁ , a₂ , …, a_n , where each represents a point at coordinate (i, a_i ). n vertical lines are drawn such that the two endpoints of line i is at (i, a_i ) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

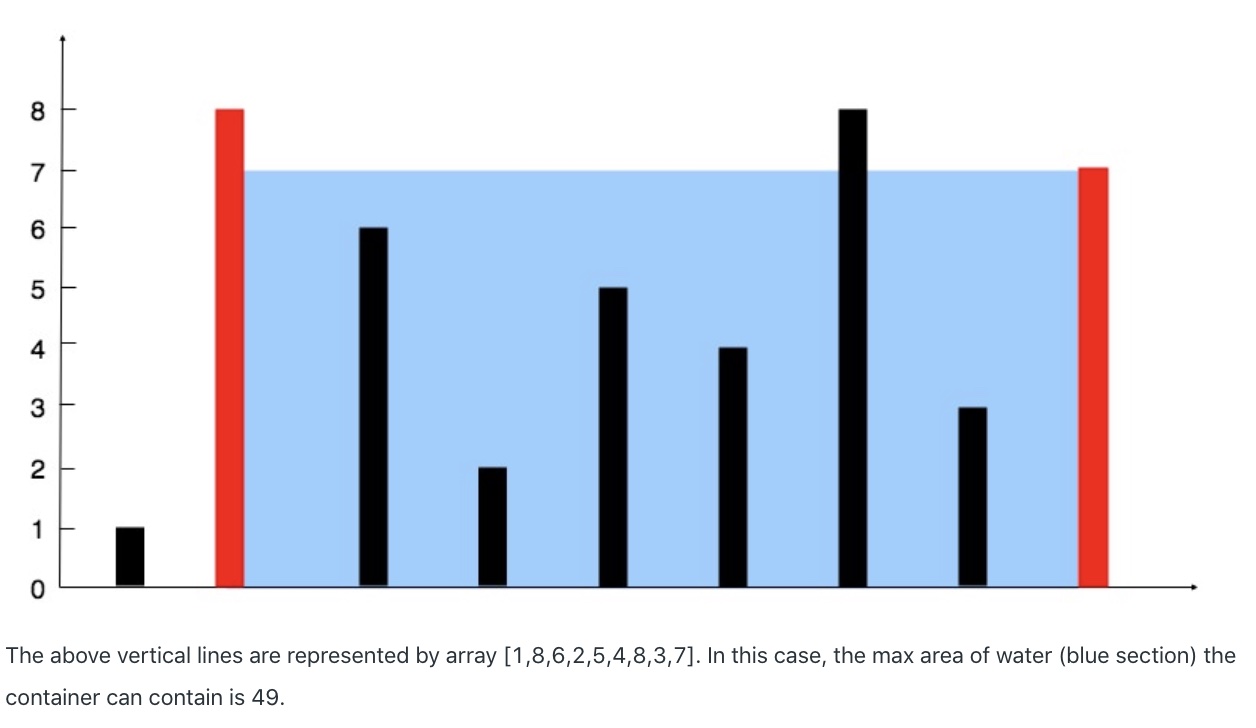
Example:

Input: [1,8,6,2,5,4,8,3,7]
Output: 49

Analysis

Basically ,we can use two pointer from start and the end of the array to scan it. The insight here is that the factor that affect the area is the minHeight, so that we can move the smaller one between left and right until it meets a higher one, then we check if the area is bigger and update values.

Here’s the code:

public class ContainerWithMostWater {
  public int maxArea(int[] height) {
    int left = 0, right = height.length - 1;
    int curLeft = left, curRight = right;
    boolean shouldMoveLeft = height[left] < height[right];
    int max = (right - left) * Math.min(height[left], height[right]);

    while (curLeft < curRight){
      if (shouldMoveLeft){
        curLeft++;
        if (height[curLeft] > height[left]){
          int newMax = (curRight - curLeft) * Math.min(height[curLeft], height[curRight]);
          if (newMax > max){
            max = newMax;
            left = curLeft;
          }

          shouldMoveLeft = height[curLeft] < height[curRight];
        }
      }
      else {
        curRight--;
        if (height[curRight] > height[right]){
          int newMax = (curRight - curLeft) * Math.min(height[curLeft], height[curRight]);
          if (newMax > max){
            max = newMax;
            right = curRight;
          }

          shouldMoveLeft = height[curLeft] < height[curRight];
        }
      }
    }

    return max;
  }
}

There is a much simple solution with same logic and more calculation:

class Solution {
    public int maxArea(int[] height) {
      if (height == null || height.length == 0) {
        return 0;
      }

      int start = 0;
      int end = height.length - 1;
      int maxArea = Integer.MIN_VALUE;

      while (start < end) {
        int sValue = height[start];
        int eValue = height[end];
        maxArea = Math.max(maxArea, (Math.min(sValue, eValue) * (end - start)));
        if (sValue < eValue) {
          start++;
        } else {
          end--;
        }
      }

      return maxArea;
    }
  }

What to improve

• should write a simple code which is easy to understand, the curLeft and curRight is useless.