LeetCode - Largest Rectangle in Histogram

Problem description

description

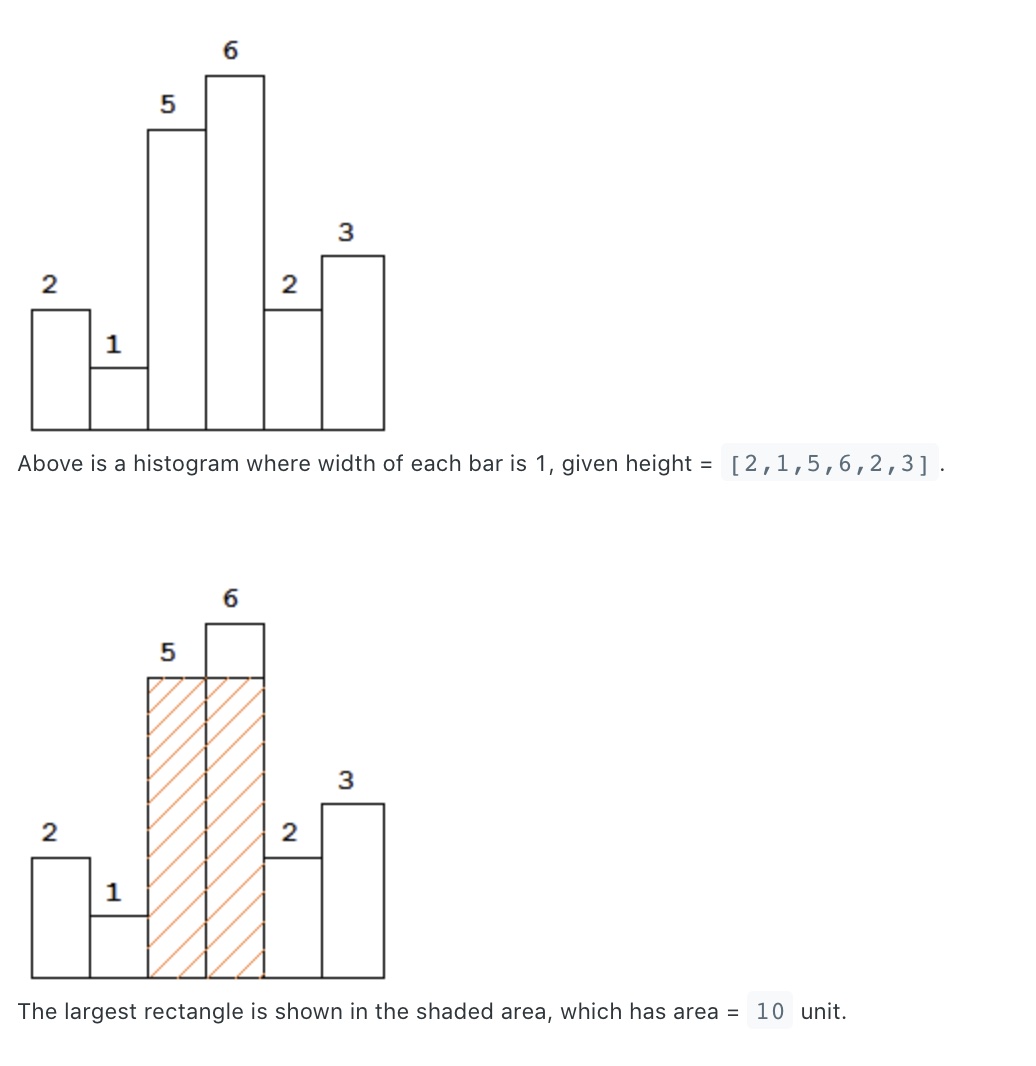
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

Example:

Input: [2,1,5,6,2,3]
Output: 10

Analysis

The first thought is to use left min and right min, and found it wrong.

Then I came up with the solution with 2-d dp, where dp[i][j] means the min height from i to j. And got MLE.

public int largestRectangleArea(int[] heights) {
        int l = 0, h = heights.length - 1;
        int len = heights.length;
        
        if (len == 0){
            return 0;
        }
        
        int[][] dp = new int[len][len];
        
        for (int i = 0; i < len;i++){
            int min = Integer.MAX_VALUE;
            for (int j = i; j < len; j++){
                dp[i][j] = Math.min(min, heights[j]);
                min = dp[i][j];
            }
        }
            
        int max = Integer.MIN_VALUE;
        
        for (int i = 0; i < len; i++){
            // int min = Integer.MAX_VALUE;
            for (int j = i; j < len ; j++){
                // min = Math.min(min, heights[j]);
                max = Math.max(max, min * (j - i + 1));
            }
        }
        
        
        return max;
    }

A better dp without extra memory is:

public int largestRectangleArea(int[] heights) {
        int l = 0, h = heights.length - 1;
        int len = heights.length;
        
        if (len == 0){
            return 0;
        }
            
        int max = Integer.MIN_VALUE;
        
        for (int i = 0; i < len; i++){
            int min = Integer.MAX_VALUE;
            for (int j = i; j < len ; j++){
                min = Math.min(min, heights[j]);
                max = Math.max(max, min * (j - i + 1));
            }
        }
        
        
        return max;
    }

Another method is using divide and conquer.

We can translate this into three sub-problem. The maximum area is consist of three situation:

1. The widest possible rectangle with height equal to the height of the shortest bar.

2. The largest rectangle confined to the left of the shortest bar(subproblem).

3. The largest rectangle confined to the right of the shortest bar(subproblem).

So:

public class Solution {
    public int calculateArea(int[] heights, int start, int end) {
        if (start > end)
            return 0;
        int minindex = start;
        for (int i = start; i <= end; i++)
            if (heights[minindex] > heights[i])
                minindex = i;
        return Math.max(heights[minindex] * (end - start + 1), Math.max(calculateArea(heights, start, minindex - 1), calculateArea(heights, minindex + 1, end)));
    }
    public int largestRectangleArea(int[] heights) {
        return calculateArea(heights, 0, heights.length - 1);
    }
}

A final solution with O(n) TC with explanation.

Basically, for each column in array with index i, the maximum area contains that column is (r-l+1) * height[i], where r is the last one bigger than or equal to height[i] start from i towards right, l is the last one bigger than or equal to height[i] start from i towards left.

And we can let l and r be the first one smaller than height[i] from index i, and the max area should be (r-1 -(l+1) + 1) = (r-l-1).

And we can use lessFromLeft array to find the next p, where lessFromLeft[i] means the first one smaller than i.

from this version of code:

for (int i = 1; i < height.length; i++) {              
    int p = i - 1;
    while (p >= 0 && height[p] >= height[i]) {
        p--;
    }
    lessFromLeft[i] = p;              
}

to:

while (p >= 0 && height[p] >= height[i]) {
      p = lessFromLeft[p];
}

And the whole solution:

public static int largestRectangleArea(int[] height) {
    if (height == null || height.length == 0) {
        return 0;
    }
    int[] lessFromLeft = new int[height.length]; // idx of the first bar the left that is lower than current
    int[] lessFromRight = new int[height.length]; // idx of the first bar the right that is lower than current
    lessFromRight[height.length - 1] = height.length;
    lessFromLeft[0] = -1;

    for (int i = 1; i < height.length; i++) {
        int p = i - 1;

        while (p >= 0 && height[p] >= height[i]) {
            p = lessFromLeft[p];
        }
        lessFromLeft[i] = p;
    }

    for (int i = height.length - 2; i >= 0; i--) {
        int p = i + 1;

        while (p < height.length && height[p] >= height[i]) {
            p = lessFromRight[p];
        }
        lessFromRight[i] = p;
    }

    int maxArea = 0;
    for (int i = 0; i < height.length; i++) {
        maxArea = Math.max(maxArea, height[i] * (lessFromRight[i] - lessFromLeft[i] - 1));
    }

    return maxArea;
}

What to improve

• think carefully and then code

• null check