LeetCode - Sudoku Solver
Problem description
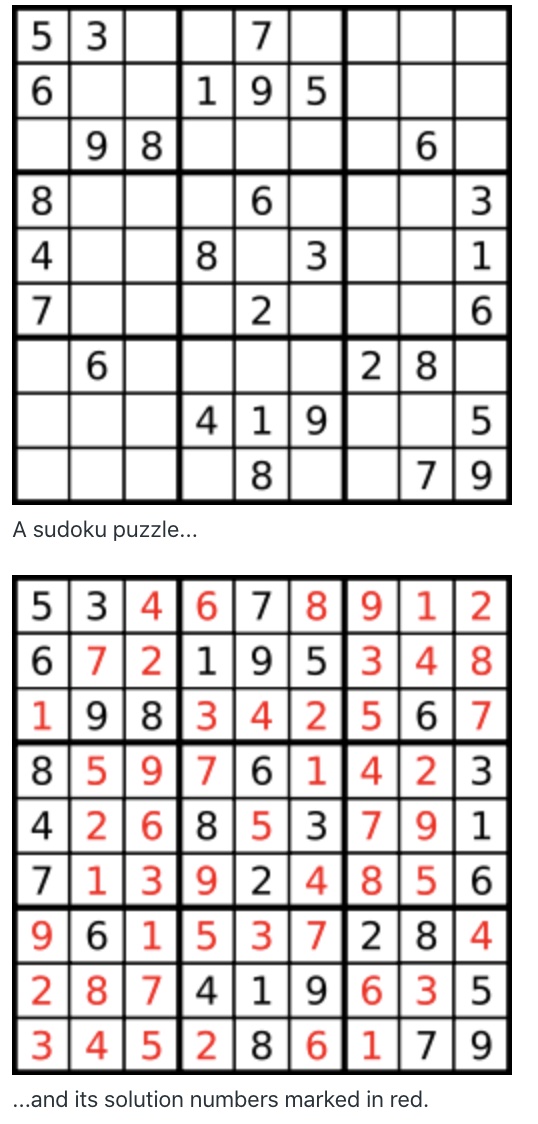
Write a program to solve a Sudoku puzzle by filling the empty cells.
A sudoku solution must satisfy all of the following rules:
- Each of the digits 1-9 must occur exactly once in each row.
- Each of the digits 1-9 must occur exactly once in each column.
- Each of the the digits 1-9 must occur exactly once in each of the 9 3x3 sub-boxes of the grid.
Empty cells are indicated by the character ‘.’.
Note:
- The given board contain only digits 1-9 and the character ‘.’.
- You may assume that the given Sudoku puzzle will have a single unique solution.
- The given board size is always 9x9.
Analysis
Just use the backtrack.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
public class SudokuSolver {
static int N = 9;
char[][] board;
int[][] rows = new int[N][N];
int[][] cols = new int[N][N];
int[][] boxes = new int[N][N];
boolean solved = false;
public void solveSudoku(char[][] board) {
this.board = board;
fillExistNumber(board);
backtrack(0, 0);
if (solved){
fillSolution();
}
}
void fillSolution() {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
board[i][j] = (char) (rows[i][j] + '0');
}
}
}
void backtrack(int i, int j) {
if (i == N && j == 0) {
solved = true;
return;
}
if (rows[i][j] != 0) {
j++;
if (j == N) {
j = 0;
i++;
}
backtrack(i, j);
} else {
List<Integer> avail = findAvailable(i, j);
for (int val : avail) {
if (solved){
break;
}
fillNumber(i, j, val);
j++;
if (j == N) {
j = 0;
i++;
}
backtrack(i, j);
if (!solved) {
j--;
if (j < 0) {
j = N - 1;
i--;
}
while (!couldRemove(i ,j)){
j--;
if (j < 0) {
j = N - 1;
i--;
}
}
removeNumber(i, j);
}
}
}
}
boolean couldRemove(int i, int j){
return board[i][j] == '.';
}
List<Integer> findAvailable(int i, int j) {
List<Integer> list = new ArrayList<>();
for (int k = 1; k <= N; k++) {
if (isRowAvailable(i, j, k) && isColAvailable(i, j, k) && isBoxAvailable(i, j, k)) {
list.add(k);
}
}
return list;
}
boolean isRowAvailable(int i, int j, int val) {
for (int k = 0; k < N; k++) {
if (rows[i][k] == val) {
return false;
}
}
return true;
}
boolean isColAvailable(int i, int j, int val) {
for (int k = 0; k < N; k++) {
if (cols[j][k] == val) {
return false;
}
}
return true;
}
boolean isBoxAvailable(int i, int j, int val) {
int boxIndex = i / 3 * 3 + j / 3;
for (int k = 0; k < N; k++) {
if (boxes[boxIndex][k] == val) {
return false;
}
}
return true;
}
void fillExistNumber(char[][] board) {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (board[i][j] != '.') {
int val = board[i][j] - '0';
fillNumber(i, j, val);
}
}
}
}
void fillNumber(int i, int j, int val) {
rows[i][j] = val;
cols[j][i] = val;
int boxRow = i / 3;
int boxCol = j / 3;
int boxIndex = boxRow * 3 + boxCol;
int innerIndex = (i - boxRow * 3) * 3 + j - boxCol * 3;
boxes[boxIndex][innerIndex] = val;
}
void removeNumber(int i, int j) {
rows[i][j] = 0;
cols[j][i] = 0;
int boxRow = i / 3;
int boxCol = j / 3;
int boxIndex = boxRow * 3 + boxCol;
int innerIndex = (i - boxRow * 3) * 3 + j - boxCol * 3;
boxes[boxIndex][innerIndex] = 0;
}
}
This solution is slow, a better solution is to use three boolean to find whether a number is available.
Here’s the code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
// row[i][j] indicate that in row i, value j is used or not
boolean[][] rows = new boolean[9][10], cols = new boolean[9][10], boxes=new boolean[9][10];
public void solveSudoku(char[][] board) {
for(int i=0; i<9; i++){
for(int j=0; j<9; j++){
if(board[i][j] != '.'){
int n = board[i][j]-'0';
int area = (i/3)*3 + j/3;
rows[i][n] = cols[j][n] = boxes[area][n] = true;
}
}
}
fill(board, 0, 0);
}
public boolean fill(char[][] board, int r, int c){
if(r==9) return true;
int nc = (c+1) % 9;
int nr = (nc==0) ? r+1 : r;
if(board[r][c] != '.') return fill(board, nr, nc);
int area = (r/3)*3 + c/3;
for(int i=1; i<=9; i++){
if(!rows[r][i] && !cols[c][i] && !boxes[area][i]) {// here we can know that i is available.
rows[r][i] = cols[c][i] = boxes[area][i] = true;
board[r][c] = (char)(i + '0');
if(fill(board, nr, nc)) return true;
board[r][c] = '.';
rows[r][i] = cols[c][i] = boxes[area][i] = false;
}
}
return false;
}
}
What to improve
- some thing can be reuseable should be saved to improve performance