LeetCode - The Bit Manipulation Part

Single Number Problem

reference

Problem description

“Given an array of integers, every element appears k (k > 1) times except for one, which appears p times (p >= 1, p % k != 0). Find that single one.”

The basic idea to solve this problem is to use calculate each position’s 1’s. Let’s say we have a k = 3 and p = 1 single number problem. Then if we count the 1’s number in each bit. The count would be 3 * x+1 if the single one is 1 at that bit and would be 3 * x if the single one is 0 at that bit. So we can get the single one.

And to do this calculation, we can use bit manipulation to do this. The basic idea is to use m different counters where 2^m >= k, so that we can describe k in binary form. If we have a 1 in a specific bit for the incoming interger in array, we can add 1 to the counter, and do the add 1 operation for each counter. The picture below describe how it works.

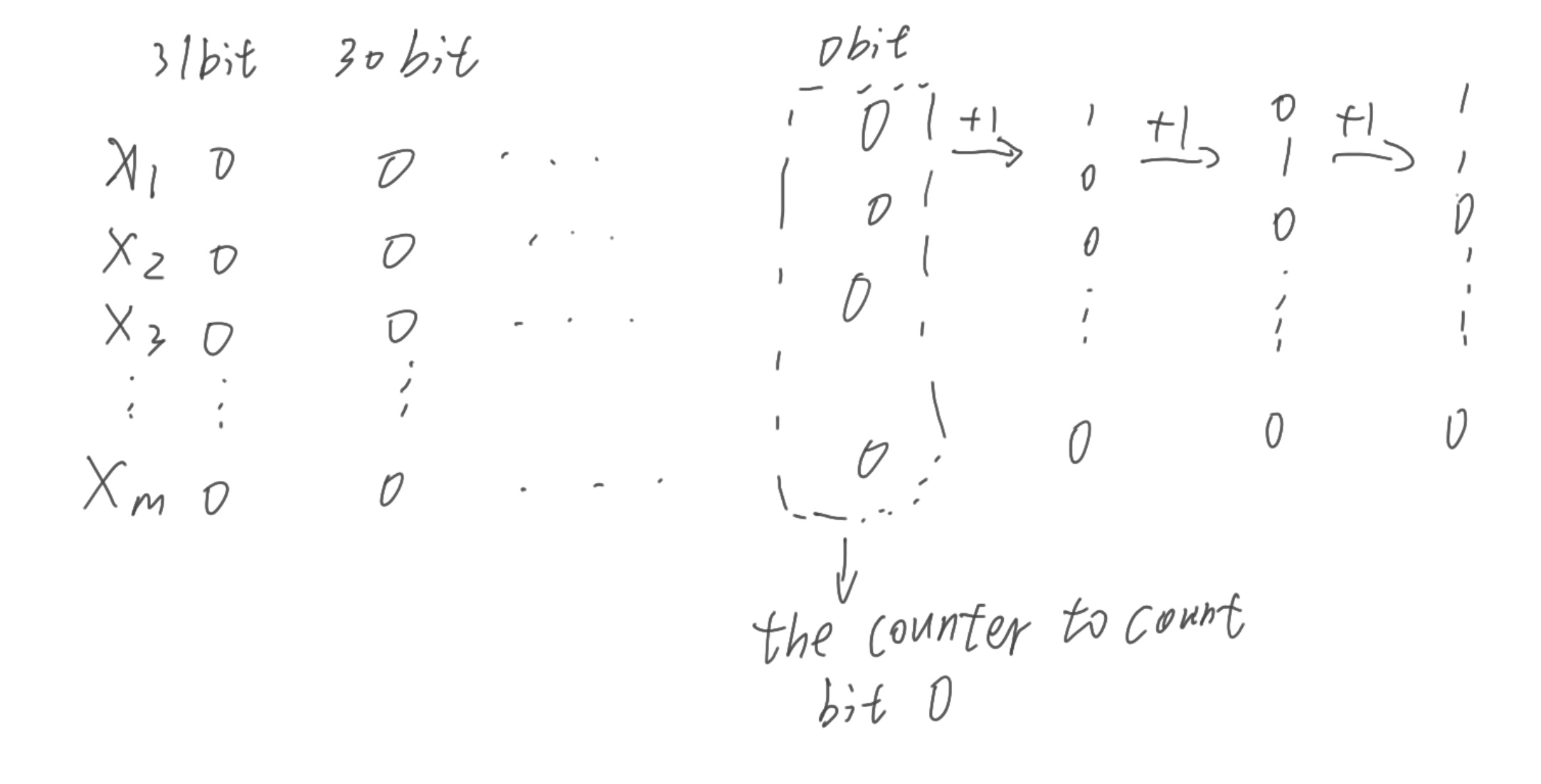
And if we have a k <= 2^m, then we need a mask to change the counter into 0 only if it reaches k. And that mask should be the opposite of the binary form of k in (km … k1) form. For example, if k is 5, then binary form of k is (101), and the opposite of k would be ~(x3 & ~x2 & x1), where the first 1 devotes to x3, the first 0 devotes to the ~x2, and the second 1 devotes to x1.

and this mask would be 0 only if xm … x1 represents k in binary form. Otherwise, it would be 1 so that if we use this mask to do & operation with x1 to xm, the value won’t change and we can simulate a mod operation.

Template:

for (int i : nums) {
    xm ^= (xm-1 & ... & x1 & i);
    xm-1 ^= (xm-2 & ... & x1 & i);
    .....
    x1 ^= i;
    
    mask = ~(y1 & y2 & ... & ym) where yj = xj if kj = 1, and yj = ~xj if kj = 0 (j = 1 to m).

    xm &= mask;
    ......
    x1 &= mask;
}

return x1 | x2 ... | xm; // the other number repeated k times is devotes 0 to the xi since we masked them.

Other Bit related problems

reference reference2

• Use the properties of x & (-x) to get the rightmost 1.

we know that -x is (~x+1), so for a integer forms like …100000..00 in binary form. If we do ~(invert) operation and wo got something like …011111..11 in binary form. If we add 1, it would be …100000..00. So we can have a integer inverted before the rightmost 1 and the same as x after rightmost 1 inclusively.

So that we can have a x & (-x) to get the rightmost 1 of x. And we can do something use this property. For example, to check if x is the power of 2, we can check (x&(-x)) == x.

• Use the properties of x & (x-1) to hide the rightmost 1.

If we minus 1 for x, then the rightmost 1 with following 0 would be 0111…, and if we do & with x, then we remove the rightmost 1 successfully.